|
| Лена Глазунова | Тема не совсем оффтопиковая, вполне биологическая, но лучше пусть здесь будет.
Короче, мне опять нужна помощь коллективного разума. 
Когда-то у меня было всё в порядке с математикой и мозгами, я без проблем пользовалась критерием согласия Пирсона, и всё понимала. Причём я до сих пор умею им пользоваться. Ну, по крайней мере, для элементарных случаев. Но вот в мозгу что-то сломалось, и я утратила понимание одного важного момента. Читаю книгу, не понимаю. Спросила коллегу, похоже и её сломала своими дурацкими вопросами. Никто не вставит мне выпавший кусок мозга на место? 
Нулевая гипотеза: расхождения случайны.
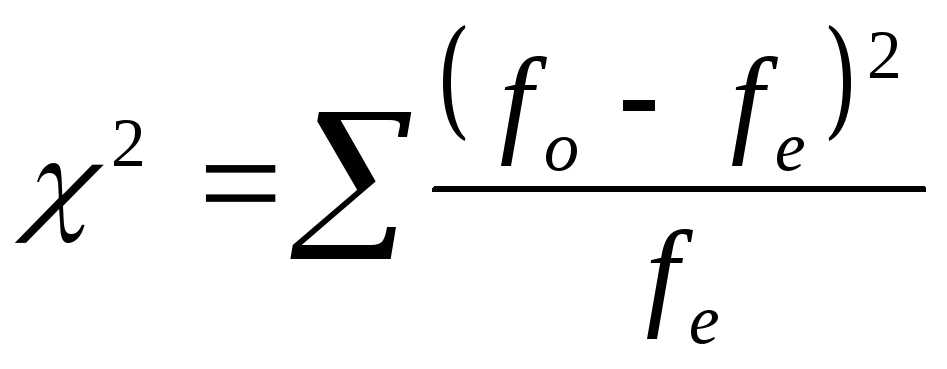
Чем меньше расхождения, тем меньшее значение критерия получается. Это понятно. Есть критическое значение хи-квадрат, с ним и сравниваем. Если у нас получилось меньше, чем критическое значение для данного числа степеней свободы и уровня значимости, значит нулевую гипотезу принимаем с данным уровнем значимости, расхождения случайны. Всё понятно, окей.
А теперь вопрос. Вот у нас таблица критических значений.
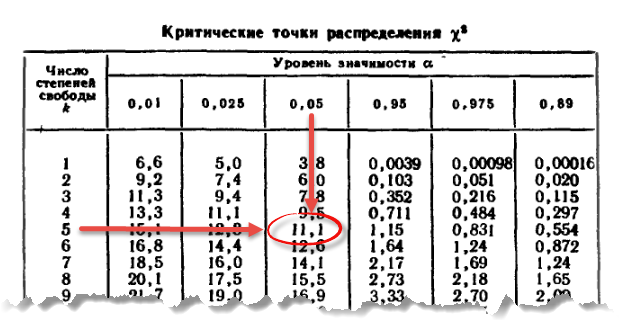
Уровень значимости — это (100% — вероятность того, что гипотеза верна). То есть вероятность ошибки, или вероятность отбросить правильную гипотезу. Так?
Как же получается, что критическое значение для α=0,05 меньше, чем для α=0,01? Это ж выходит, что проще добиться верности гипотезы с вероятностью 99%, чем 95%? То есть гипотеза не проходит с вероятностью 95%, но проходит с вероятностью 99%????
 Где я туплю? 
У меня уже была идея, что инопланетяне выкрали все правильные таблицы хи-квадрат и подсунули неправильные  | | Андрей Ковальчук | Так-с, что-то тут нечисто.
Лена Глазунова пишет:Если у нас получилось меньше, чем критическое значение для данного числа степеней свободы и уровня значимости, значит нулевую гипотезу принимаем с данным уровнем значимости, расхождения случайны. Всё понятно, окей.
С этим согласен, вроде всё правильно.
Лена Глазунова пишет:Уровень значимости — это (100% — вероятность того, что гипотеза верна).
А это откуда следует? По-моему, это утверждение и сбивает с толку.
Лена Глазунова пишет:Уровень значимости — это... вероятность отбросить правильную гипотезу. Так?
Насколько я понимаю, тут нужно уточнение - не просто правильную гипотезу, а нулевую гипотезу в случае её правильности. Так как обычно этот тест используется, чтобы показать, что расхождения не случайны, то чем меньше уровень значимости (т.е. чем больше расхождение), тем меньше вероятность, что отбрасываемая нулевая гипотеза (расхождения случайны) всё-таки верна. Как-то так, по-моему. | | Юрий Постников | Гм-м...
Гм-мур..
Гмур-ман, да
 | | Лена Глазунова | Андрей Ковальчук пишет:А это откуда следует? По-моему, это утверждение и сбивает с толку.
Ну, согласна, это я слишком упростила.
Андрей Ковальчук пишет:Насколько я понимаю, тут нужно уточнение - не просто правильную гипотезу, а нулевую гипотезу в случае её правильности.
Ну да.
Андрей Ковальчук пишет:Так как обычно этот тест используется, чтобы показать, что расхождения не случайны, то чем меньше уровень значимости (т.е. чем больше расхождение), тем меньше вероятность, что отбрасываемая нулевая гипотеза (расхождения случайны) всё-таки верна.
Эммм. Мне вроде показалось, что я поняла, но я подумала, и поняла, что ничего не понимаю 
Я исхожу из того, что
Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна
Я помню, как нас ругали за уровень значимости 0,05 — мол, это "ниачём", не очень достоверно. А при 0,01 ваша гипотеза не проходит, мол. Но тут же такого быть не может??? Может, дело в том, что обычно использовали критерий как раз для того, чтобы доказать различие выборок?
Надо подумать в это сторону...
Юрий Постников пишет:Гм-м...
Гм-мур..
Гмур-ман, да

? | | Андрей Ковальчук | Лена Глазунова пишет:Эммм. Мне вроде показалось, что я поняла, но я подумала, и поняла, что ничего не понимаю  Я исхожу из того, что
Я исхожу из того, что
Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна
Примерно это я и пытался сказать, только, наверное, коряво получилось.
Лена Глазунова пишет:Я помню, как нас ругали за уровень значимости 0,05 — мол, это "ниачём", не очень достоверно. А при 0,01 ваша гипотеза не проходит, мол. Но тут же такого быть не может??? Может, дело в том, что обычно использовали критерий как раз для того, чтобы доказать различие выборок?
Надо подумать в это сторону...
Не совсем понял, чего именно здесь не может быть. Понятно, что чем меньше уровень значимости, тем статистически достовернее наблюдаемые отличия. Если в конкретном случае они "тянут" на 0.01, то можно указать это значение, если же на 0.01 "не тянут", а "тянут" только на 0.05 - приходится с этим жить.  | | Лена Глазунова | Андрей Ковальчук пишет:Примерно это я и пытался сказать, только, наверное, коряво получилось.
Да нет, всё нормально и не коряво, это я ещё раз повторяю, чтобы в голове отпечаталось крепче 
Я, кажется, понимаю. Во-первых, у меня в голове засело сильно упрощённое понятие об уровне значимости. И о том, что чем он меньше, тем лучше. Тогда как
Различные значения α-уровня имеют свои достоинства и недостатки. Меньшие α-уровни дают бо́льшую уверенность в том, что уже установленная альтернативная гипотеза значима, но при этом есть больший риск не отвергнуть ложную нулевую (или отвергнуть истинную альтернативную) гипотезу (ошибка второго рода, или «ложноотрицательное решение»), и таким образом меньшая статистическая мощность. Выбор α-уровня неизбежно требует компромисса между значимостью и мощностью, и следовательно между вероятностями ошибок первого и второго рода.
Задачи бывают двух типов. Получается, что то, что я помнила, относилось не к расщеплениям (там мы хотим доказать нулевую гипотезу), а к доказательству эффективности чего-нибудь (мы заинтересованы в верности альтернативной гипотезы)...
Вообще странно, что я этого не замечала  | | Андрей Ковальчук | Ну да, я тоже чаще сталкиваюсь со случаями, когда нулевую гипотезу (о том, что расхождения случайны) надо, по возможности, опровергнуть. А в применении к расщеплениям в скрещиваниях я этот тест уже очень давно не использовал. | | Юрий Постников | насчет Гмурмана:
 | | Лена Глазунова | Юрий Постников пишет:насчет Гмурмана
Ааа! Ясно. Не, я точно такое не читала. У нас Лакин был. "Биометрия" Что-то ещё тоже было, но не помню уже.
Андрей, спасибо! Кажется, улеглось. Правда, надо теперь получше въехать в плюсы и минусы разных уровней альфа  |
|
 Когда-то у меня было всё в порядке с математикой и мозгами, я без проблем пользовалась критерием согласия Пирсона, и всё понимала. Причём я до сих пор умею им пользоваться. Ну, по крайней мере, для элементарных случаев. Но вот в мозгу что-то сломалось, и я утратила понимание одного важного момента. Читаю книгу, не понимаю. Спросила коллегу, похоже и её сломала своими дурацкими вопросами. Никто не вставит мне выпавший кусок мозга на место?
Когда-то у меня было всё в порядке с математикой и мозгами, я без проблем пользовалась критерием согласия Пирсона, и всё понимала. Причём я до сих пор умею им пользоваться. Ну, по крайней мере, для элементарных случаев. Но вот в мозгу что-то сломалось, и я утратила понимание одного важного момента. Читаю книгу, не понимаю. Спросила коллегу, похоже и её сломала своими дурацкими вопросами. Никто не вставит мне выпавший кусок мозга на место?  Нулевая гипотеза: расхождения случайны.
Нулевая гипотеза: расхождения случайны.
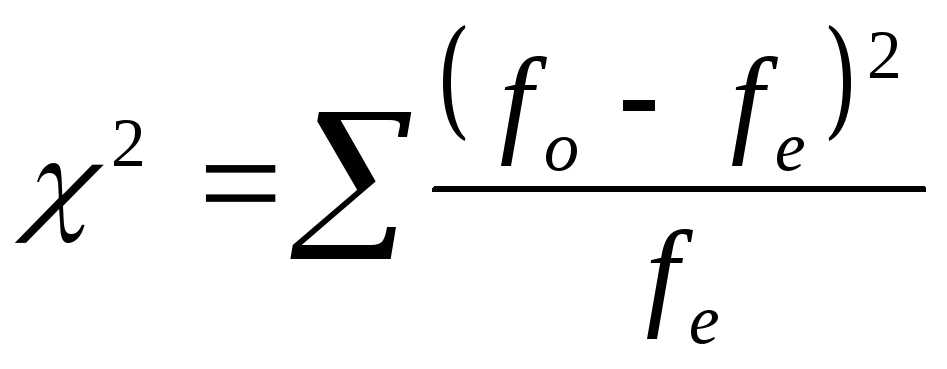 Чем меньше расхождения, тем меньшее значение критерия получается. Это понятно. Есть критическое значение хи-квадрат, с ним и сравниваем. Если у нас получилось меньше, чем критическое значение для данного числа степеней свободы и уровня значимости, значит нулевую гипотезу принимаем с данным уровнем значимости, расхождения случайны. Всё понятно, окей.
А теперь вопрос. Вот у нас таблица критических значений.
Чем меньше расхождения, тем меньшее значение критерия получается. Это понятно. Есть критическое значение хи-квадрат, с ним и сравниваем. Если у нас получилось меньше, чем критическое значение для данного числа степеней свободы и уровня значимости, значит нулевую гипотезу принимаем с данным уровнем значимости, расхождения случайны. Всё понятно, окей.
А теперь вопрос. Вот у нас таблица критических значений.
 Уровень значимости — это (100% — вероятность того, что гипотеза верна). То есть вероятность ошибки, или вероятность отбросить правильную гипотезу. Так?
Как же получается, что критическое значение для α=0,05 меньше, чем для α=0,01? Это ж выходит, что проще добиться верности гипотезы с вероятностью 99%, чем 95%? То есть гипотеза не проходит с вероятностью 95%, но проходит с вероятностью 99%????
Уровень значимости — это (100% — вероятность того, что гипотеза верна). То есть вероятность ошибки, или вероятность отбросить правильную гипотезу. Так?
Как же получается, что критическое значение для α=0,05 меньше, чем для α=0,01? Это ж выходит, что проще добиться верности гипотезы с вероятностью 99%, чем 95%? То есть гипотеза не проходит с вероятностью 95%, но проходит с вероятностью 99%????
 Где я туплю?
Где я туплю?  У меня уже была идея, что инопланетяне выкрали все правильные таблицы хи-квадрат и подсунули неправильные
У меня уже была идея, что инопланетяне выкрали все правильные таблицы хи-квадрат и подсунули неправильные 